克莱姆法则解线性方程组,是人类社会对于n阶线性方程组求解的一大突破,今天给大家讲解求解方法。
第一步:了解线性方程组的模型。
第二步:写出线性方程组的系数行列式。
第三步:判断系数行列式是否不等于零。
第四步:用常数列去替换系数行列式的对应列,进而解答。
第五步:写出对应的解。
步骤有些抽象,我以例题的形式给大家举列:
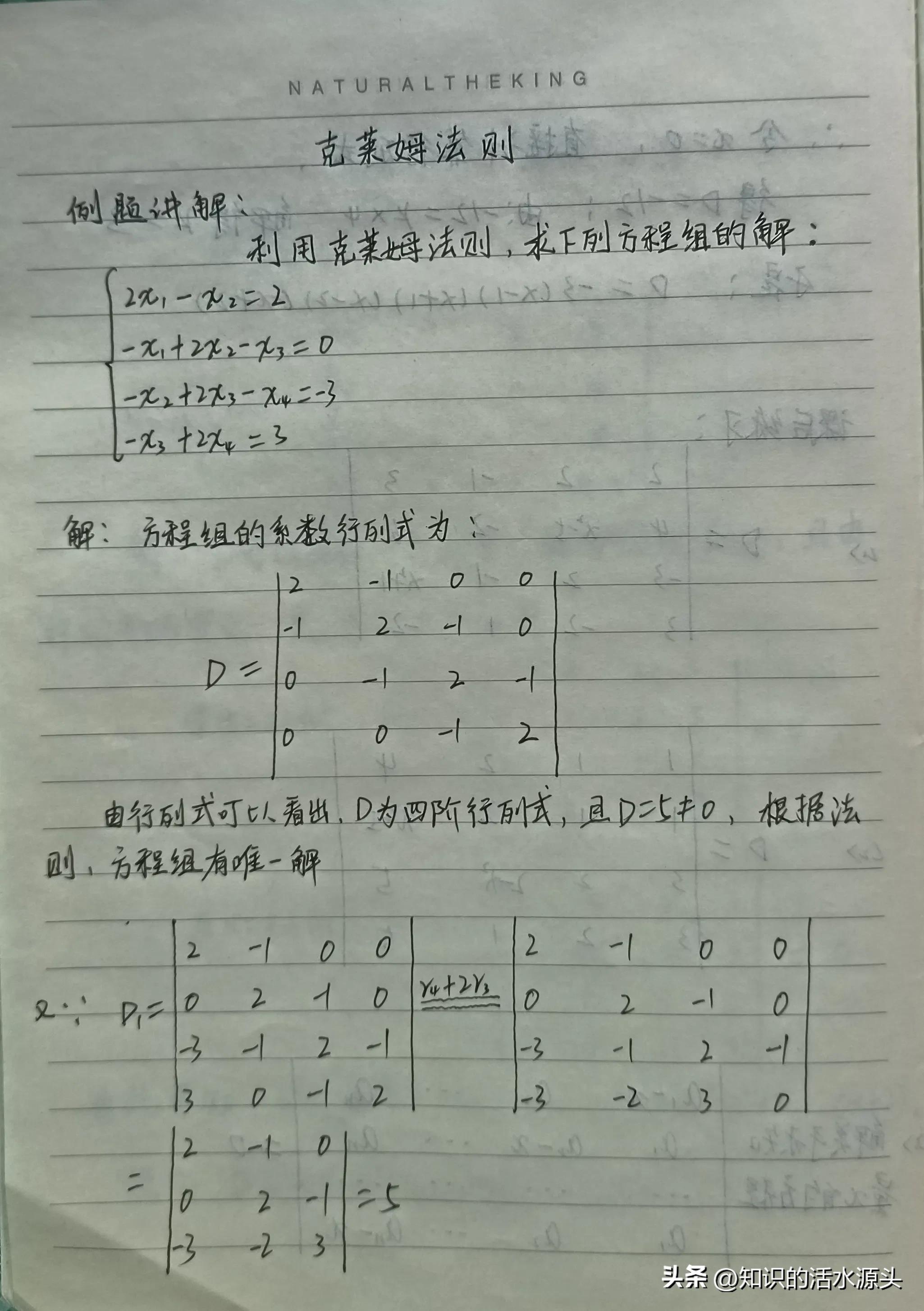


再进行计算时,除了了解步骤过后,还要注意的是,在书写系数行列式时,如果对应的未知量没有表达出来,则对应的系数元就是零
克莱姆简介:

克莱姆(Cramer, Gabriel, 1704.7.31-1752.1.4)瑞士数学家。生于日内瓦。卒于法国塞兹河畔巴尼奥勒。[1]早年在日内瓦读书,1724 年起在日内瓦加尔文学院任教,1734年成为几何学教授,1750年任哲学教授。