今天来说说关于逻辑函数的化简方法。有人说我写的过于简单,没什么用,其实一直看到现在的人应该懂,我发表的内容偏向于那些不是电气相关行业的人,想入这个坑,或者刚开始学,想提前从了解哪怕一个月后就会学到的东西,算是引导吧。
首先,关于逻辑函数的化简方法中的公式法化简:
公式法化简是利用逻辑代数基本公示,对函数进行消项、消因子(这么说有人会以为我在说数学吗...)。
常用到的有:AB+AB’=A的并项法,该公式法讲两个与项合并成为一个,从而消除另外一个变量。
A+A’B=A+B公式法用以消除与项多出的因子,此法为消因子法。
什么是消项法?即AB+A’C=AB+A’C+BC进行配项,用来消除更多的与项。
而配项法是利用A+A=A,A+A’=1的配项。
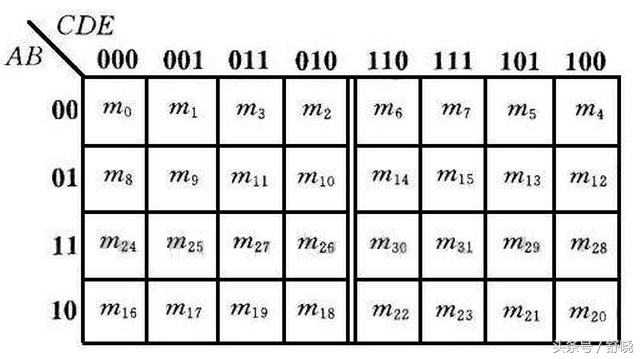
卡诺图画法
除了公式法,还有卡诺图化简法。
将n变量中的所有最小项各用一个小方块表示,并使具有逻辑相邻性(仅有一个变量不同其余变量均相同的两个最小项,称为逻辑相邻项)的最小项在几何位置上相邻排列,得到的图形叫做n变量最小项的卡诺图。
表示最小项的卡诺图
将逻辑变量分成两个组,分别在两个方向用循环码形式排列出各组变量的所有取值组合,构成一个有2n个方格的图形,每一个方格对应变量的一个取值组合。具有逻辑相邻性的最小项在位置上也相邻地排列。
用卡诺图表示逻辑函数:
方法一:1、把已知逻辑函数式化为最小项之和形式。
将函数式中包含的最小项在卡诺 图对应 的方格中填 1,其余方格中填 0。
方法二:根据函数式直接填卡诺图。
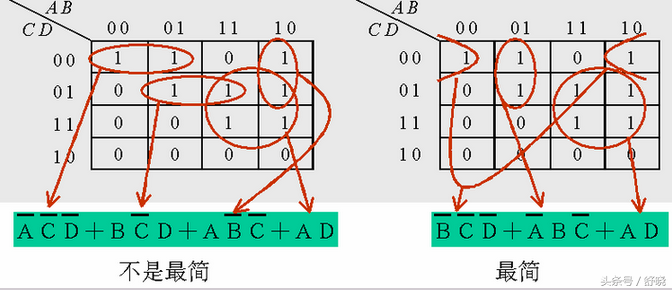
最小项的圈法需要经过比较才能确认
如何利用卡诺图化简逻辑函数:
化简依据:逻辑相邻性的最小项可以合并,并消去因子。
化简规则:能够合并在一起的最小项是2n个。
最简判断: 圈数越少越简;圈内的最小项越多越简。
合并最小项的原则:
任何两个相邻最小项,可以合并为一项,并消去一个变量。
任何4个相邻的最小项,可以合并为一项,并消去2个变量。
任何8个相邻最小项,可以合并为一项,并消去3个变量。
利用卡诺图化简逻辑函数的步骤如下:
第一步:将逻辑函数变换为最小项之和的形式
第二步:画出表示该逻辑函数的卡诺图
第三步:找出可以合并的最小项并画出合并圈
第四步:写出最简的与-或表达式
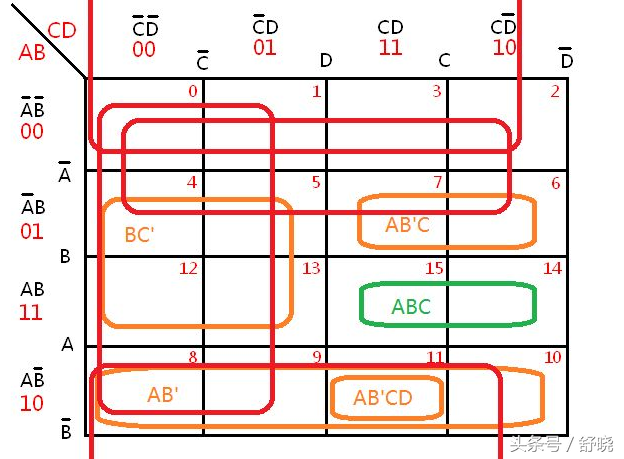
F='(ABC)+A'BCD+A'B+A'BC+B'C卡诺图化简结果F=A'+B'+C'
画出函数的卡诺图;
画圈(先圈孤立1格;再圈只有一个方向的最小项(1格)组合);
卡诺图画圈原则:合并个数为2n;圈尽可能大(乘积项中含因子数最少);圈尽可能少(乘积项个数最少);每个圈中至少有一个最小项仅被圈过一次,以免出现多余项。
注意:在卡诺图中所有的1都必须圈到, 不能合并的1单独画圈。而逻辑函数的卡诺图化简结果有可能不是唯一性的。

惯例来个脑力活动,为什么?